STAN Introduction

Joseph Sartini

2025-01-31

What is STAN?

• Bayesian probabilistic programming language

• Multiple posterior sampling routines

  • Hamiltonian Monte Carlo

  • Variational Inference

  • Laplace approximation

• Based on C++

• Interfaces with Python, Julia, R, and Unix Shell

Structure of a STAN Script

functions {
  // ... function declarations and definitions ...
}
data {
  // ... declarations ...
}
transformed data {
   // ... declarations ... statements ...
}
parameters {
   // ... declarations ...
}
transformed parameters {
   // ... declarations ... statements ...
}
model {
   // ... declarations ... statements ...
}
generated quantities {
   // ... declarations ... statements ...
}

All blocks are optional, an empty string is actually a valid STAN code. Order is important, they must be in the above order Variables have scope over all subsequent blocks

Section - functions

• Complex indexing

  • Sparsely observed data

• Generating quantities/structures

  • Splines, etc.

• Suffixes for particular functions

  • Containing RNG: “_rng”

  • Modifying target density: “_lp”

RNG functions can only be used on data/generated quantities

Section - data

• Likelihood data

  • Indexing arrays

• All constants

  • Array extents

• Commonly used linear transforms

Often need more information in this block than you think to fully specify the model.

Section - transformed data

• Functions of data variables

• Only evaluated once

  • Prior to sampling

• Helpful for book-keeping

  • Simplify data inputs

• Random data sub-samples

Section - parameters

• Specify sampled quantities

  • Variable names

  • Extents

• Definitions only, no statements

• Read from underlying sampler

• Can provide initial values

• Will get more into how to provide initial values shortly

Section - transformed parameters

• Deterministic functions

• Part of target posterior

• Evaluated with each sample

  • Inverse transform

  • Log absolute Jacobian

• Good for re-parameterization

  • Stability

  • Latent modeling

• Can include data, transformed data, and parameters as inputs

• Need inverse transform and log absolute Jacobian to be efficient, as they can greatly slow down the sampling process otherwise

• Natural scale vs sampling efficiency (NUTS and standard HMC prefer unconstrained parameters). However, gradient calculations usually dwarf these differences

Section - model

• Define the target posterior

  • Sum of log density functions

• Prior distributions on (transformed) parameters

• Data/model likelihood

• Most computational expense

• ORDER MATTERS

It is often important to know which subgroup of operations within the model block is consuming the majority of computation time (after deciding that efficient is insufficient). We will get to how this can be done (do not optimize unless necessary).

Section - generated quantities

• Executed after samples are generated

• Functions of model output

  • Predictions for new data

  • Simulate new data

  • Extract posterior estimates

  • Calculate model fit criterion

Example Model - GLM

data {
  int N;  // Number of observations
  int P;  // Number of fixed effect covariates
  
  array[N] int<lower=0, upper=1> Y;  // Binary outcomes
  matrix[N, P] X;                    // Fixed effects design matrix
}
parameters {
   vector[P] beta;  // Coefficients
}
model {
   Y ~ bernoulli_logit(X * beta);
}

While there is no explicit prior on beta here, that just means that STAN is choosing the equivalent to a uniform prior under the hood

Running the Model in R

fit_df = mtcars %>%
  mutate(Efficient = case_when(mpg >= median(mpg) ~ 1,
                               TRUE ~ 0)) %>%
  mutate(am = as.factor(am))
fit_matrix = model.matrix(~cyl + disp + hp + drat + wt + am, fit_df)

data_list = list(N = nrow(mtcars), P = ncol(fit_matrix), 
                 Y = fit_df$Efficient, X = fit_matrix)

model = sampling(
  first_model, 
  data = data_list, 
  chains = 4, 
  iter = 1000, 
  warmup = 500, 
  # init = ,
  # control = list(adapt_delta = , 
  #                max_treedepth = , 
  #                stepsize_jitter = ), 
  verbose = F,
  refresh = 0
)

Convergence Monitoring

check_hmc_diagnostics(model)

Divergences:

0 of 2000 iterations ended with a divergence.

Tree depth:

1212 of 2000 iterations saturated the maximum tree depth of 10 (60.6%).
Try increasing 'max_treedepth' to avoid saturation.

Energy:

E-BFMI indicated no pathological behavior.

summary(model)$summary[,"Rhat"]

 beta[1]  beta[2]  beta[3]  beta[4]  beta[5]  beta[6]  beta[7]     lp__ 
2.365263 2.081568 2.424803 2.459833 2.446590 1.643589 2.438779 1.039459 

Hamiltonian Monte Carlo

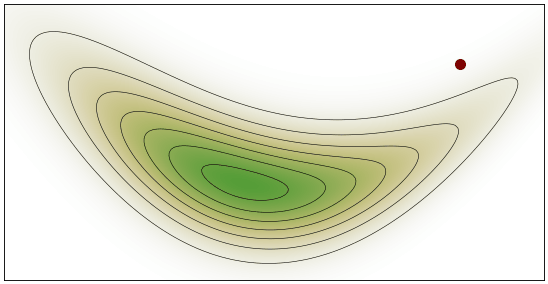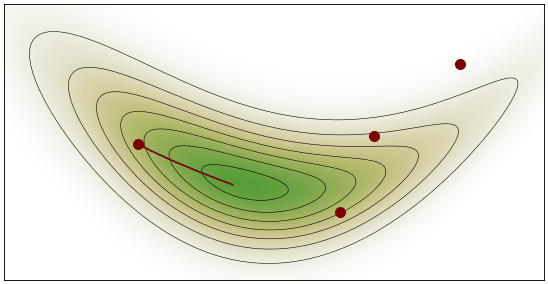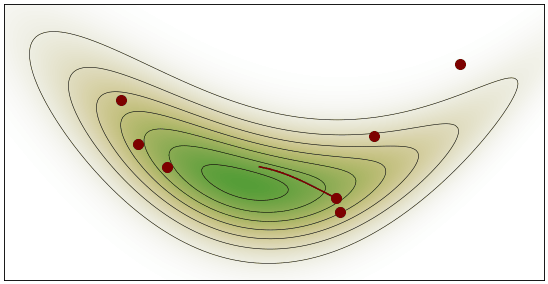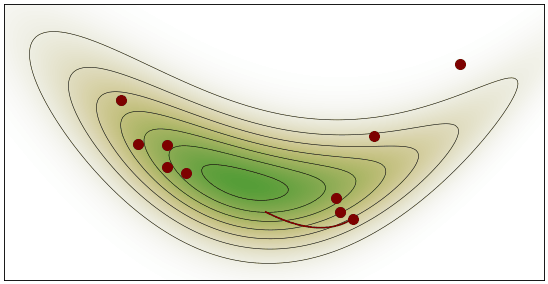
HMC Visualization: By Justinkunimune - github.com/jkunimune/hamiltonian-mc, CC0

Hamiltonian Monte Carlo Continued

• Version of Metropolis-Hastings

• Hamiltonian Dynamics used to propose next state

  • Trajectory with momentum

  • Distribution \(\approx\) potential energy field

  • Leapfrog integrator stepwise approximation

• Momentum: reduced correlation between samples

• Energy conservation: high acceptance probability

• Leapfrog integrator uses model gradient to take steps, why it is important to keep this efficient (analytical gradients built-in by STAN for many things)

• Use MH step to compensate for numerical issues in the Leapfrog algorithm, but acceptance probability should be high if things go well (not needed in perfect world)

Divergences

• Simulated trajectory \(\neq\) true trajectory

• Global step size \(>\) true posterior geometry resolution

  • Leapfrog first order approximataion

• Hamiltonian departs from initial value

  • Total energy (kinetic + potential)

  • Should be preserved along trajectory

• Sampler WILL NOT accept samples after divergence

Tree Depth Warnings

• Tree depth controls number of simulation steps

  • \(\leq 2^{max\_treedepth}\) steps

• Primarily an efficiency concern

• Generally recommended to not increase

  • Often model misspecification

Est. Bayesian Fraction of Miss. Info.

• Posterior decomposes into energy equivalence classes

• Low EBFMI indicates getting “stuck” in energy sets

  • STAN monitors energy during sampling

• Insufficiently exploring the posterior

  • Tails too large, etc

Geometric Intuition

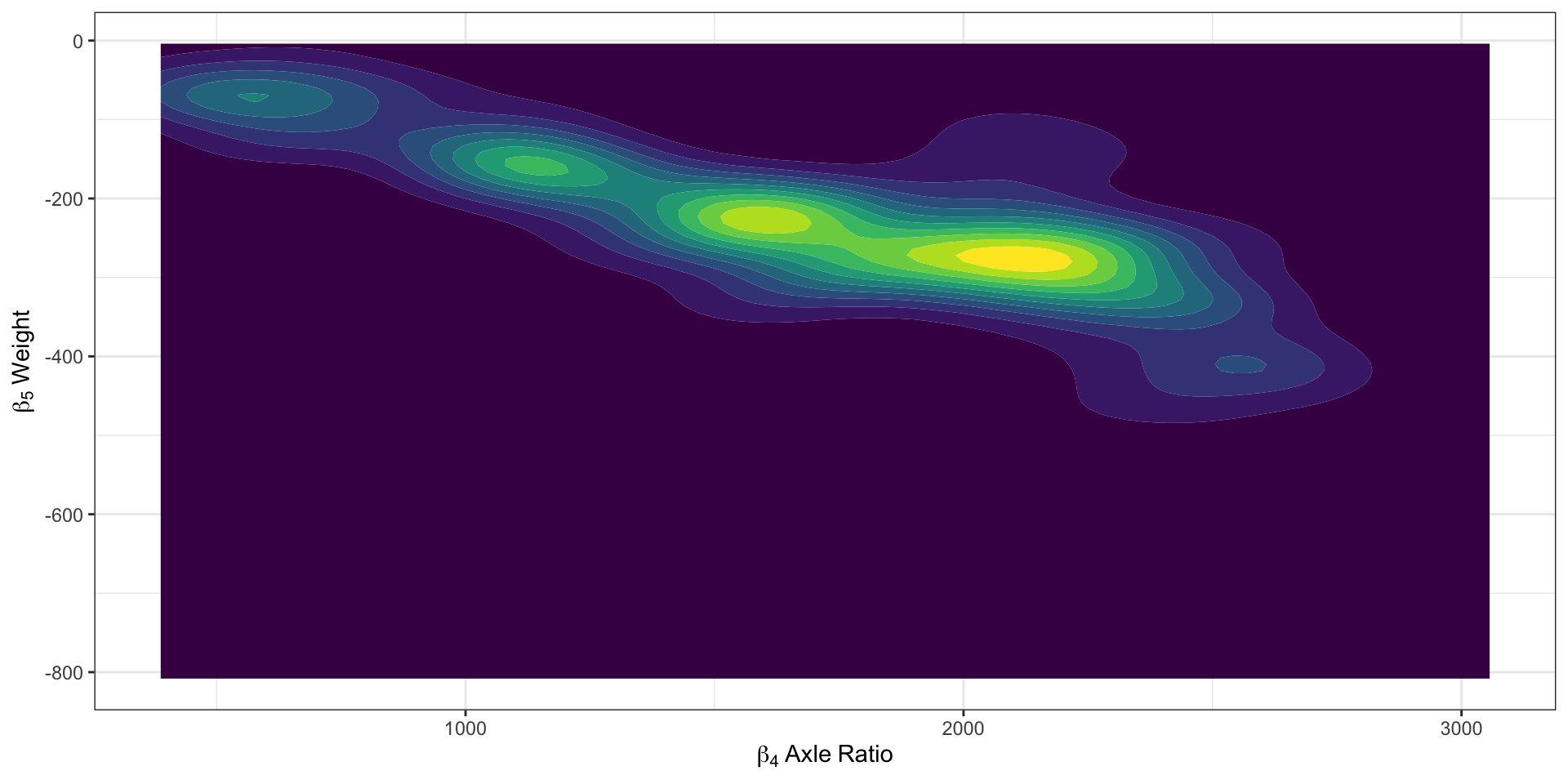
Return to our Example: Model Outputs

samples = extract(model)

beta_0 = map(1:dim(samples$beta)[1], function(x){
  return(data.frame(beta0 = samples$beta[x,1], 
                    Sample = x))
}) %>% list_rbind()

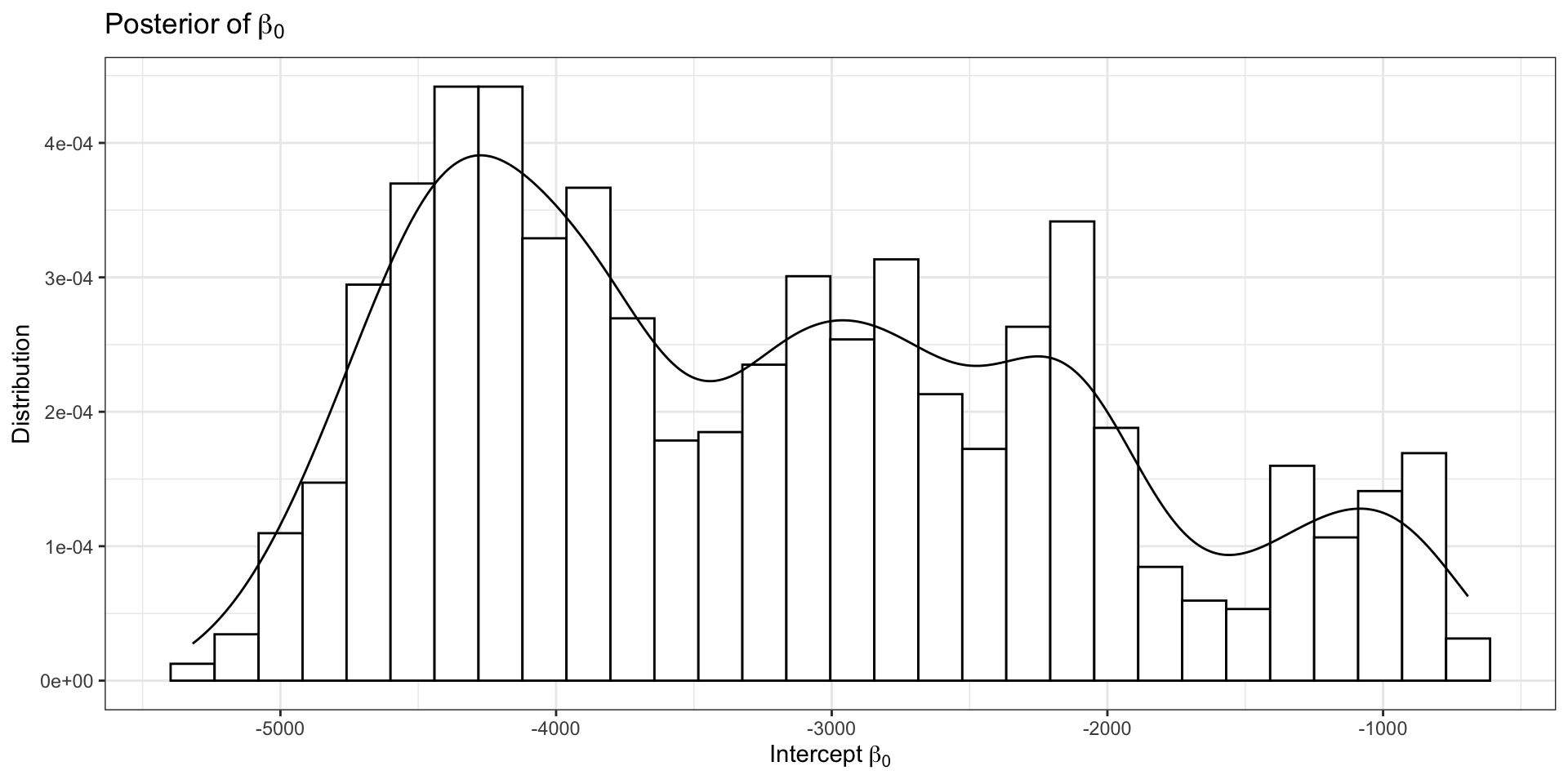
Model Outputs (2)

samples = extract(model, "beta", permuted = FALSE)

beta_0 = map(1:dim(samples)[1], function(x){
  return(data.frame(beta0 = samples[x,,1], 
                    Chain = 1:4, 
                    sample = x))
}) %>% list_rbind()

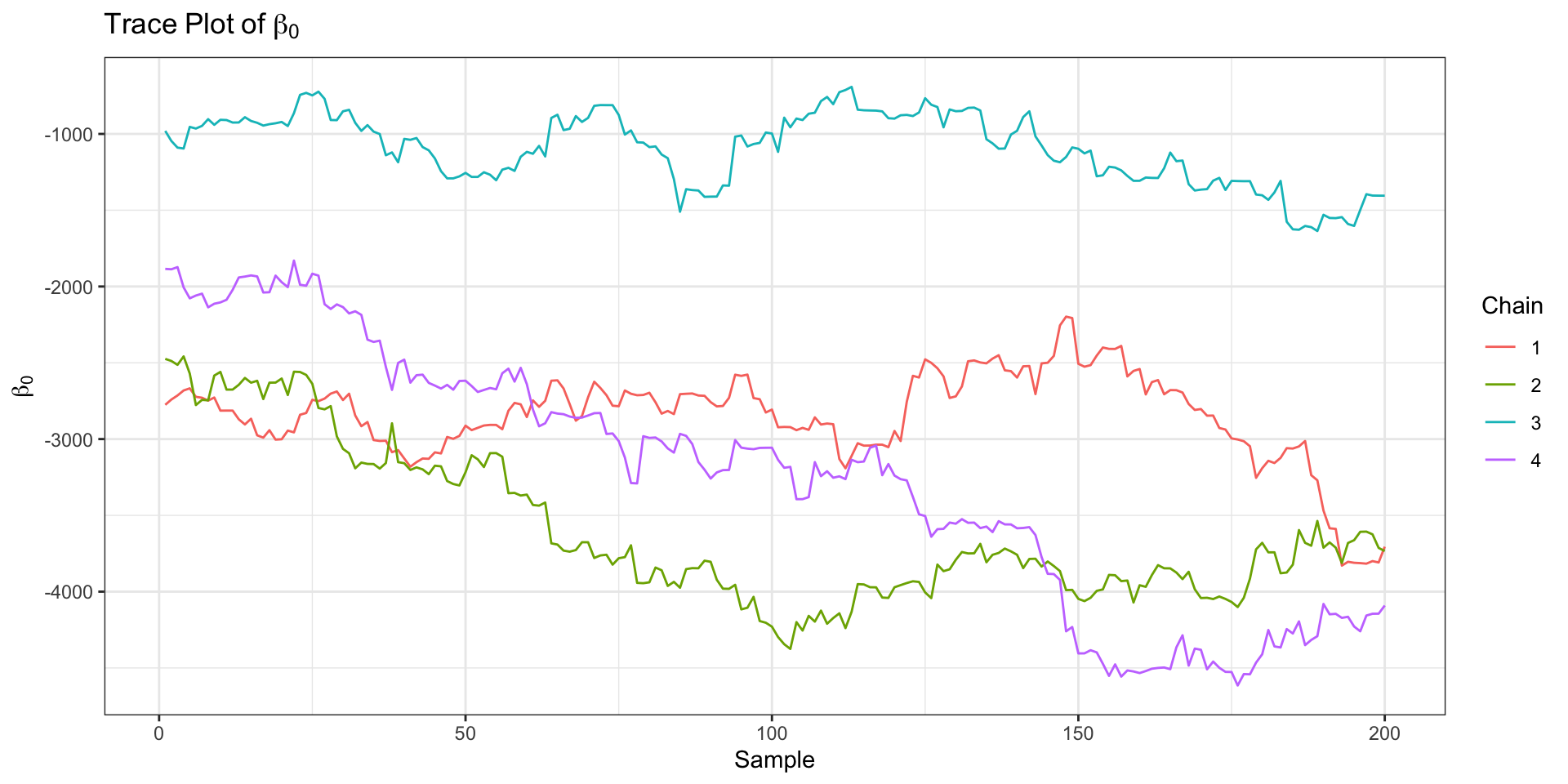
ShinySTAN Debugging

launch_shinystan(model)

ShinySTAN - NUTS Summary

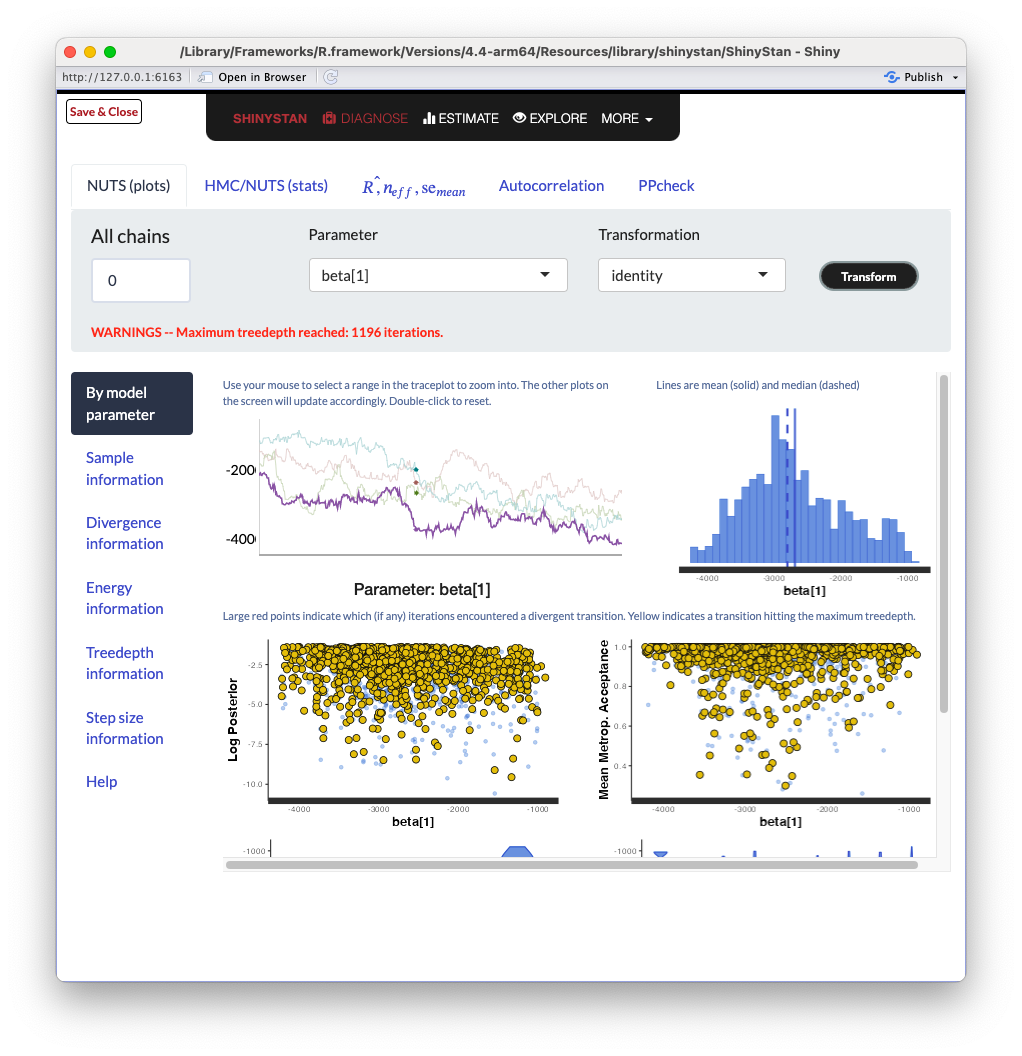
ShinySTAN - Divergences

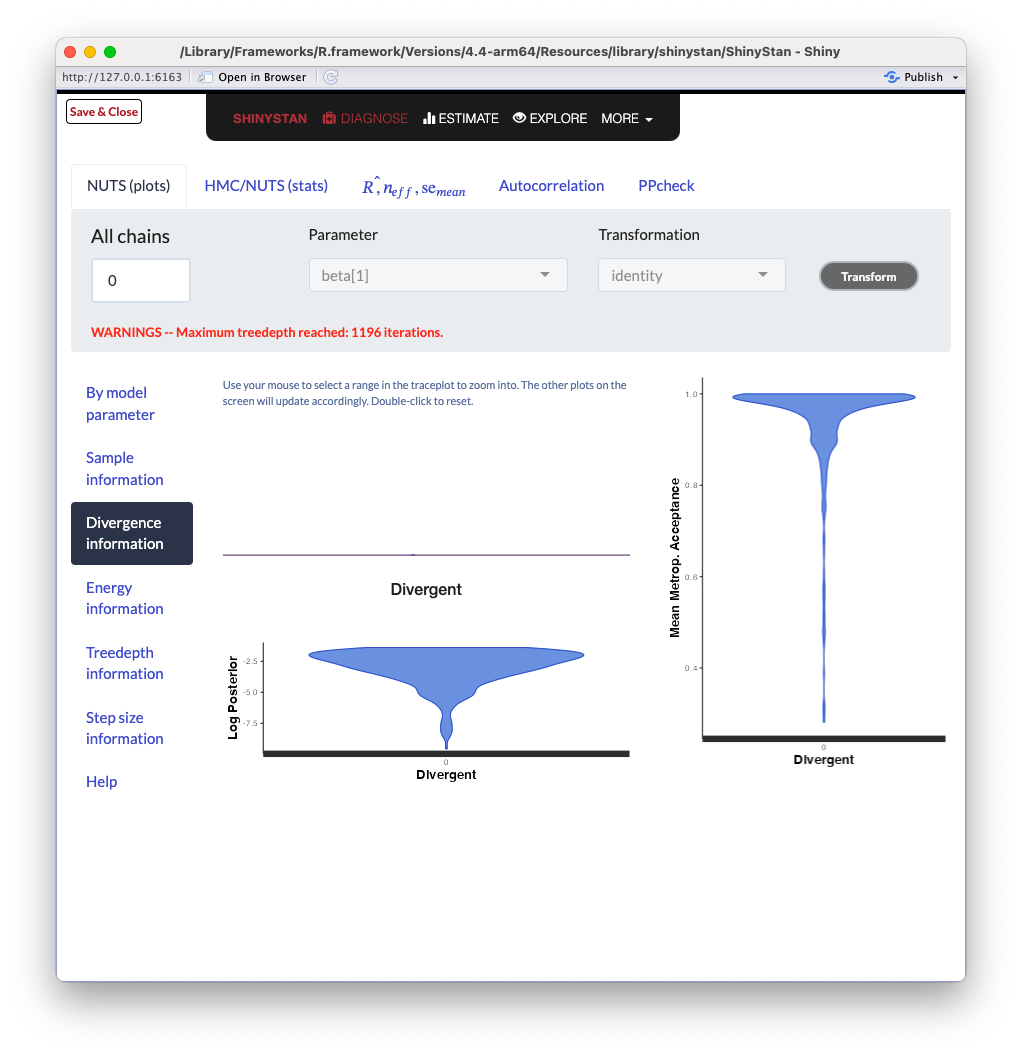
ShinySTAN - Treedepth

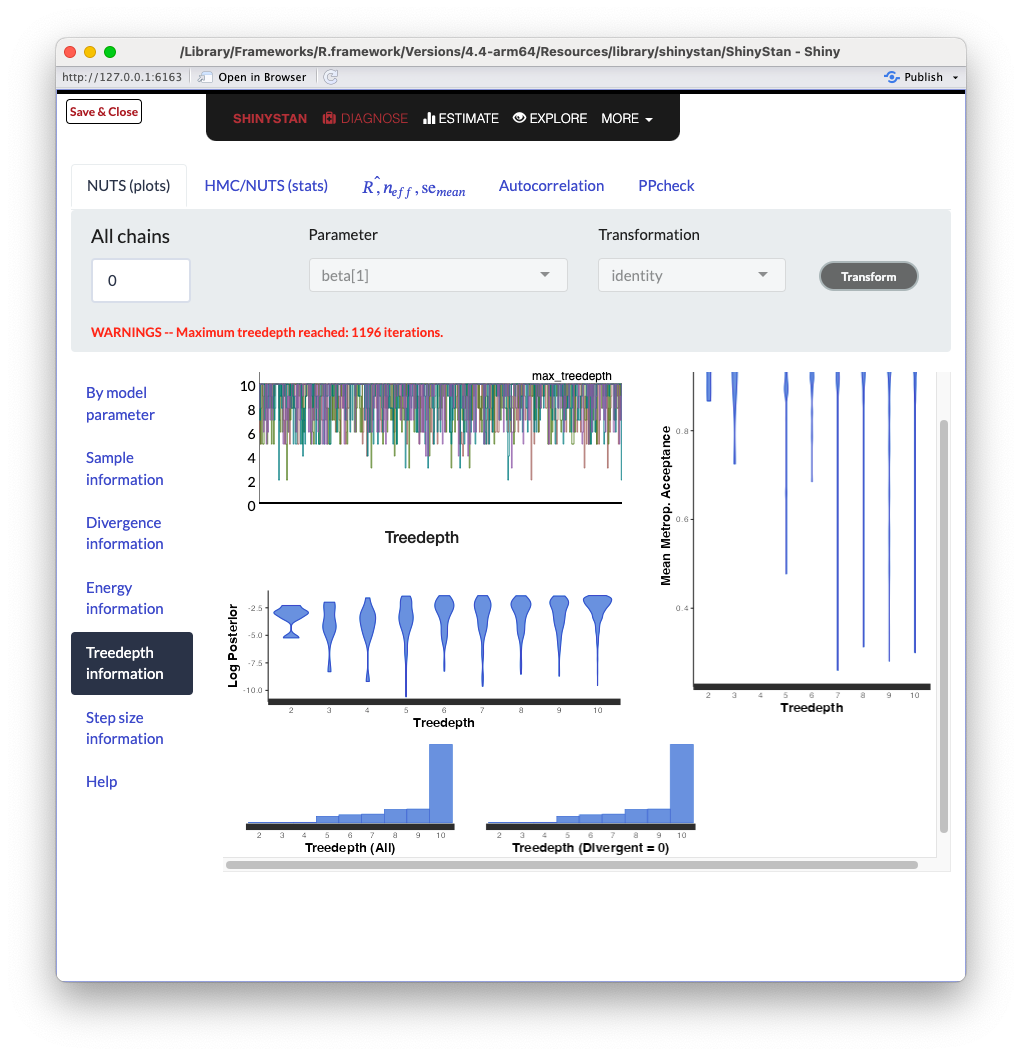
ShinySTAN - Energy

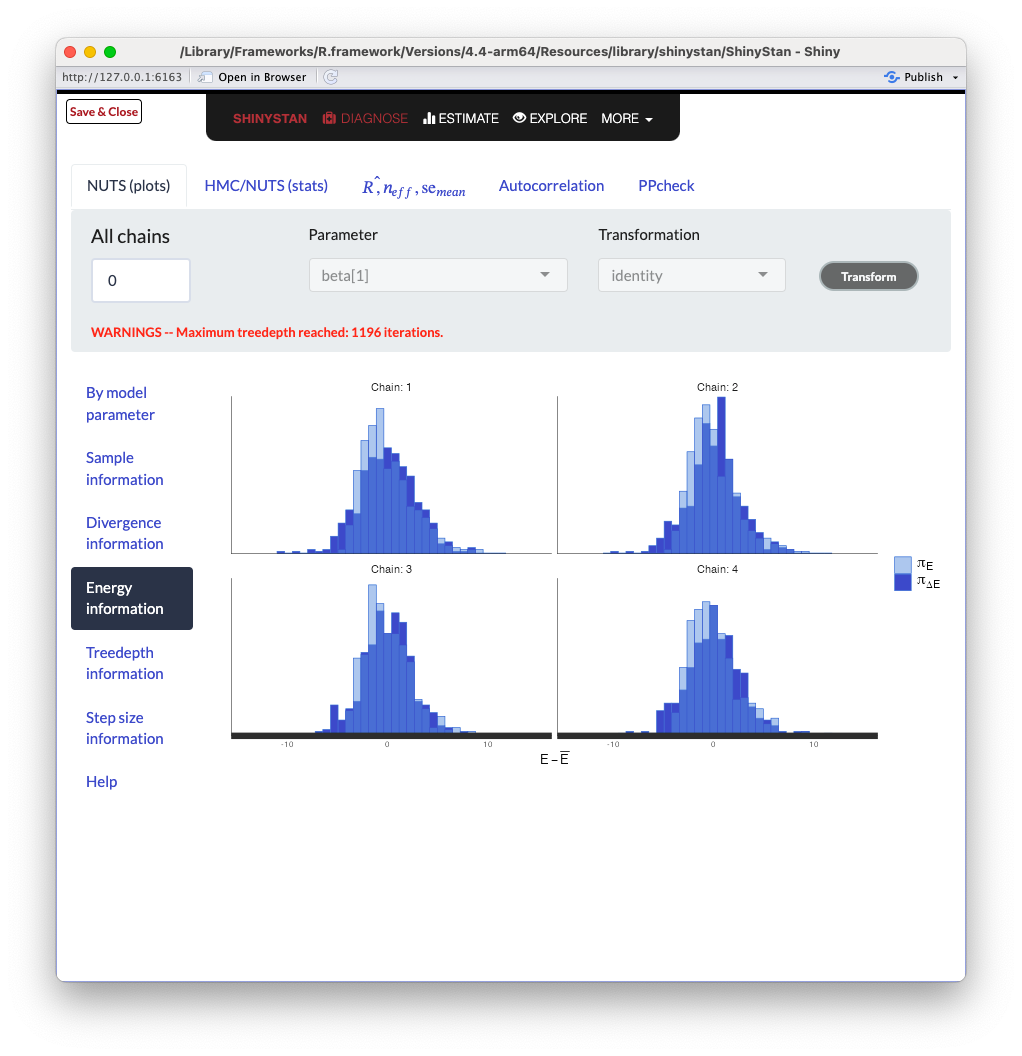
ShinySTAN - Autocorrelation

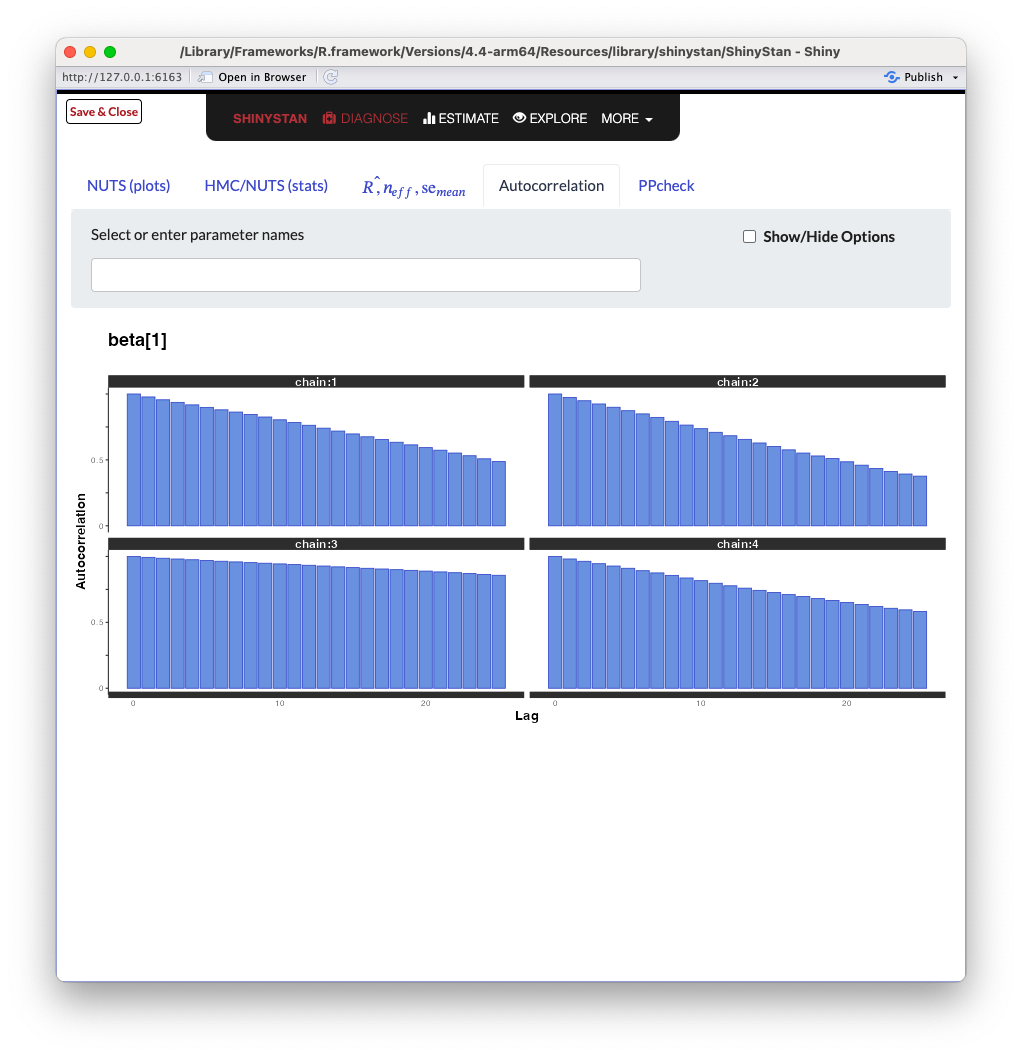
How to Update the Model

data {
  int N;  // Number of observations
  int P;  // Number of fixed effect covariates
  
  array[N] int<lower=0, upper=1> Y;  // Binary outcomes
  matrix[N, P] X;                    // Fixed effects design matrix
}
transformed data {
  matrix[N, P] Q_coef = qr_thin_Q(X) * sqrt(N-1);
  matrix[P, P] R_coef = qr_thin_R(X) / sqrt(N-1);
  matrix[P, P] R_coef_inv = inverse(R_coef);
}
parameters {
  vector[P] theta;  // Coefficients
}
model {
  theta ~ normal(0, 100);
  Y ~ bernoulli_logit(Q_coef * theta);
}
generated quantities {
  vector[P] beta = R_coef_inv * theta;
}

Running the Updated Model

model = sampling(
  second_model, 
  data = data_list, 
  chains = 4, 
  iter = 2500, 
  warmup = 1000, 
  control = list(adapt_delta = 0.95),
  verbose = F,
  refresh = 0
)

Updated Model Performance

check_hmc_diagnostics(model)

Divergences:

0 of 6000 iterations ended with a divergence.

Tree depth:

0 of 6000 iterations saturated the maximum tree depth of 10.

Energy:

E-BFMI indicated no pathological behavior.

summary(model)$summary[,"Rhat"]

theta[1] theta[2] theta[3] theta[4] theta[5] theta[6] theta[7]  beta[1] 
1.003796 1.003760 1.001931 1.003562 1.003605 1.003334 1.003570 1.002406 
 beta[2]  beta[3]  beta[4]  beta[5]  beta[6]  beta[7]     lp__ 
1.001364 1.003667 1.003591 1.003552 1.000757 1.003570 1.001324 

Updated Model Visualization

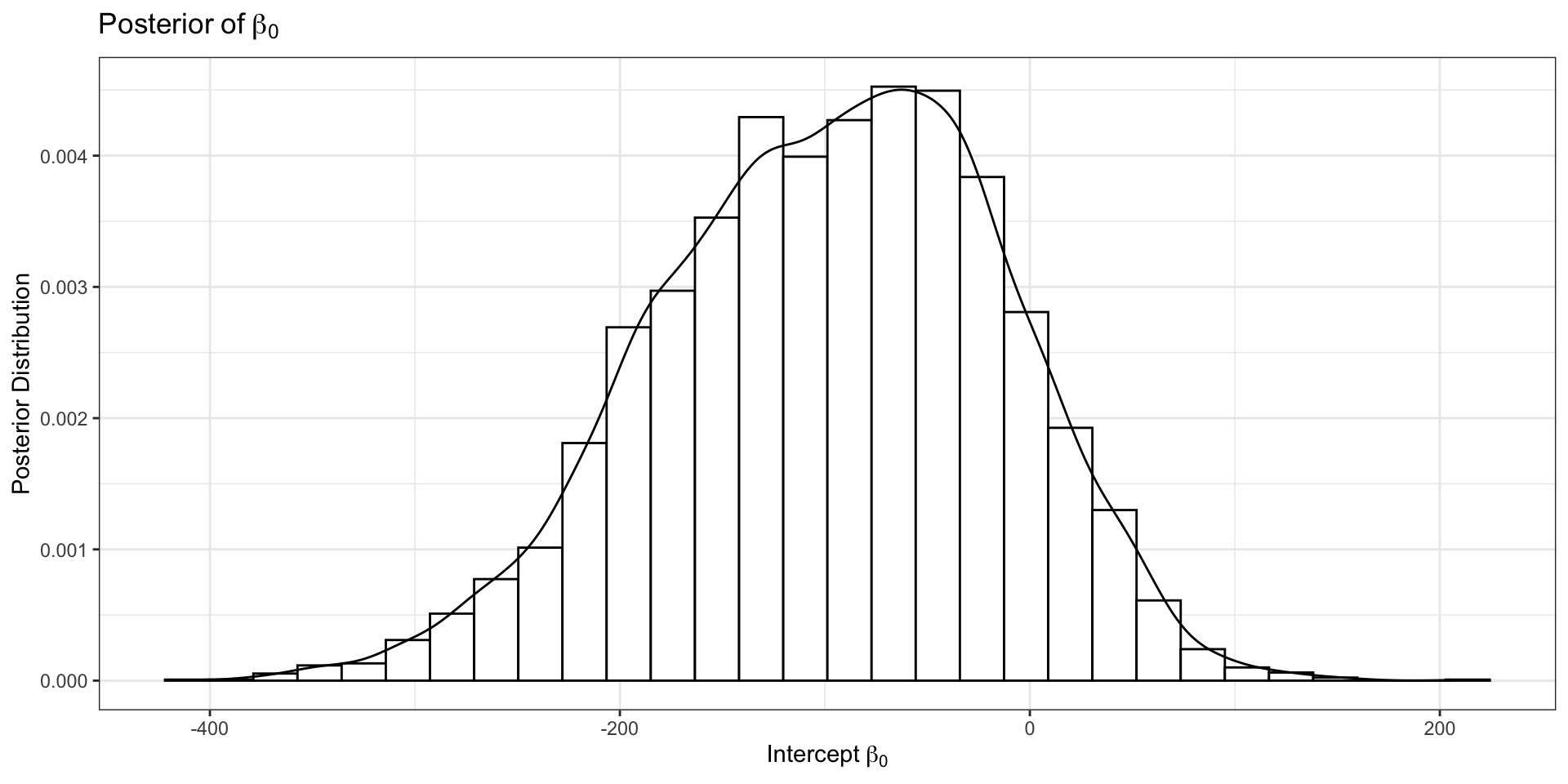
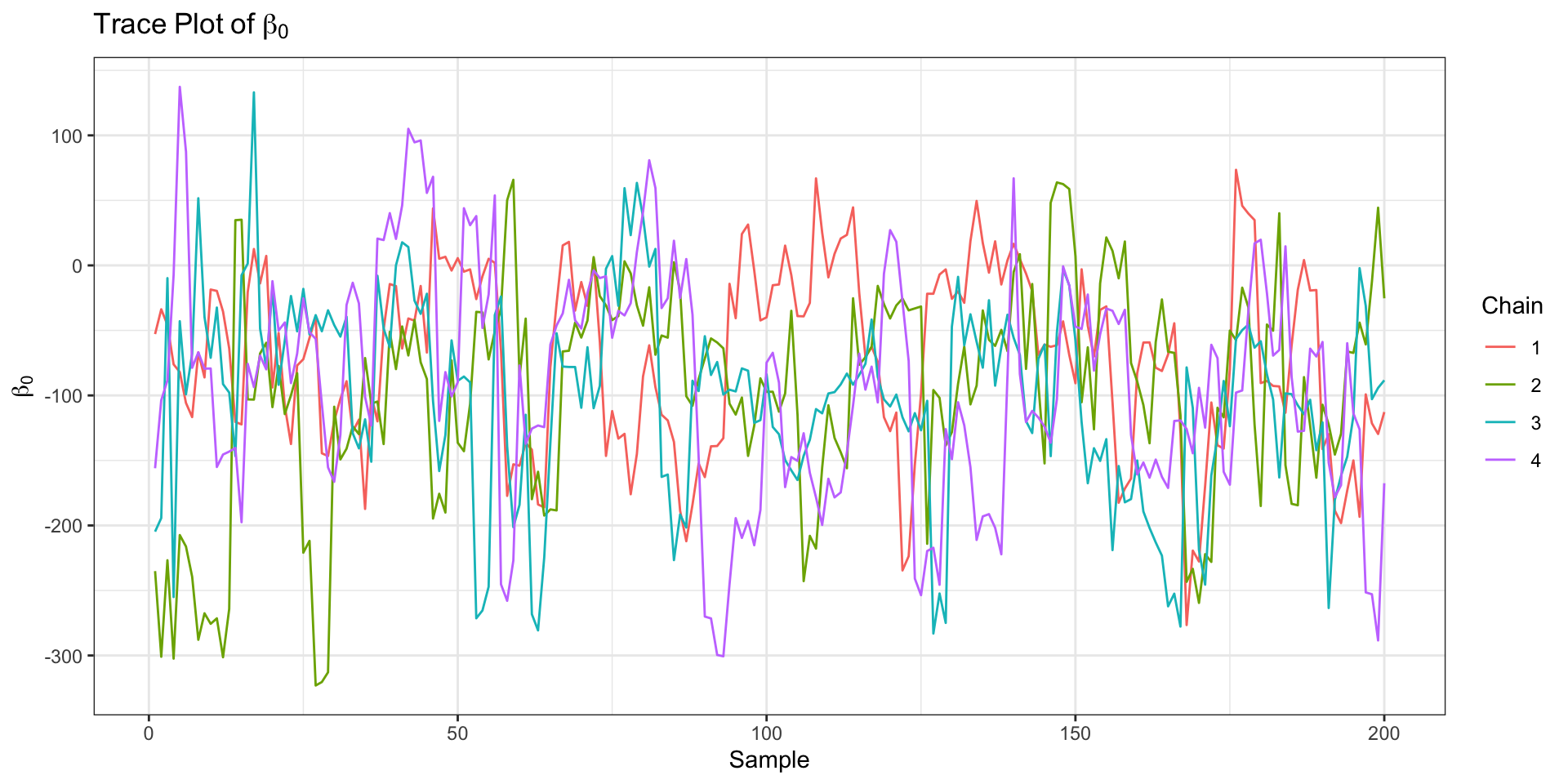
Updated Geometry

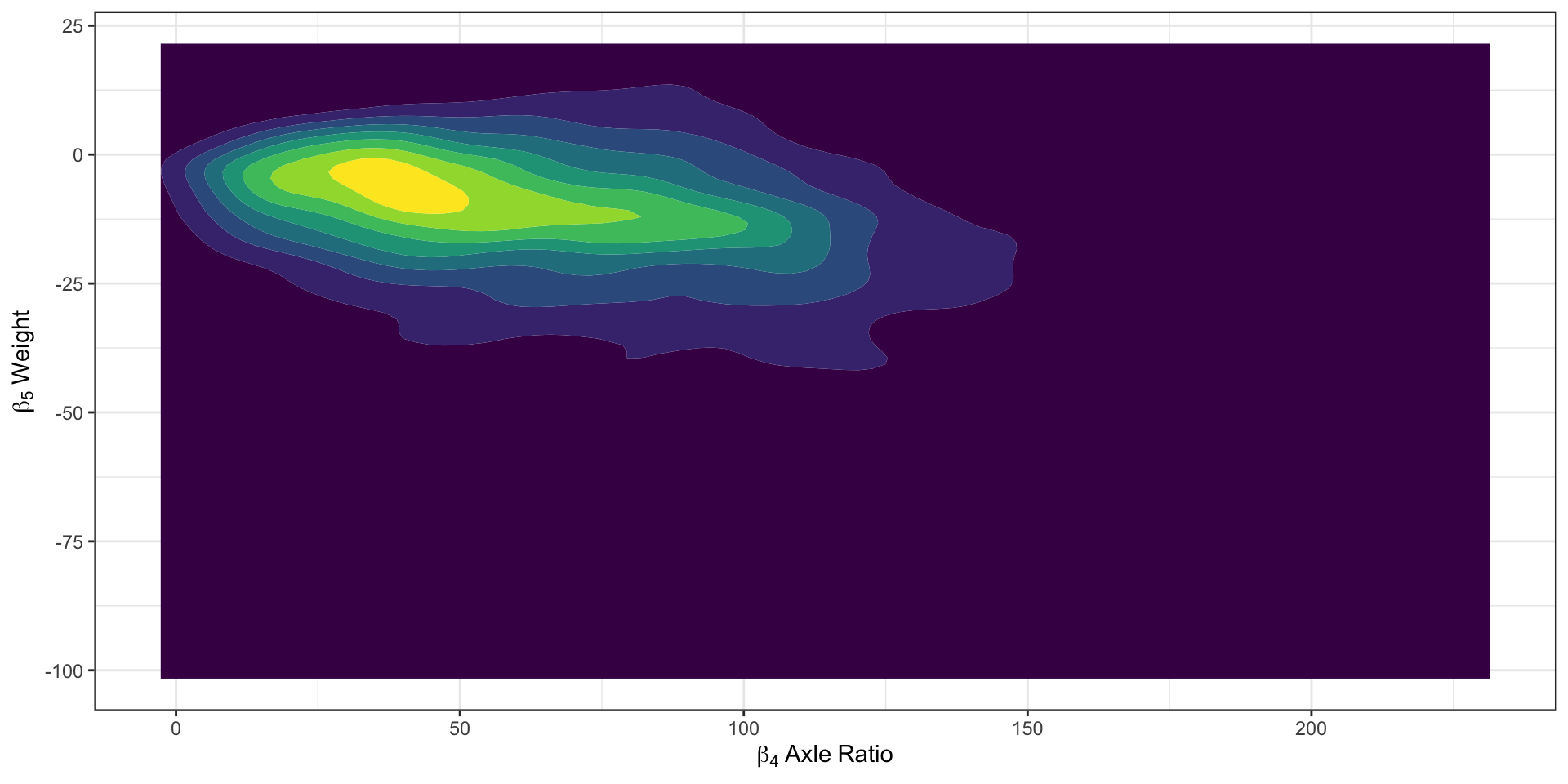
Profiling the Model with CmdStanR (1)

data {
  int N;  // Number of observations
  int P;  // Number of fixed effect covariates
  
  array[N] int<lower=0, upper=1> Y;  // Binary outcomes
  matrix[N, P] X;                    // Fixed effects design matrix
}
transformed data {
  matrix[N, P] Q_coef = qr_thin_Q(X) * sqrt(N-1);
  matrix[P, P] R_coef = qr_thin_R(X) / sqrt(N-1);
  matrix[P, P] R_coef_inv = inverse(R_coef);
}
parameters {
  vector[P] theta;  // Coefficients
}
model {
  profile("Priors") {
    target += normal_lpdf(theta| 0, 100);
  }
  profile("Likelihood") {
    target += bernoulli_logit_lpmf(Y| Q_coef * theta);
  }
}
generated quantities {
  profile("Generated") {
    vector[P] beta = R_coef_inv * theta;
  }
}

Profiling the Model with CmdStanR (2)

model = cmdstan_model("Profile_Mod.stan")
fit = model$sample(data = data_list, chains = 1)
fit$profiles()[[1]][,c(1,3,4,5,8)]

        name  total_time forward_time reverse_time autodiff_calls
1  Generated 0.000175152  0.000175152   0.00000000              0
2 Likelihood 0.145845000  0.116126000   0.02971880         170759
3     Priors 0.026700700  0.023262300   0.00343839         170759

Resource Links

• STAN Manual

• Introduction to HMC

• Bayesian Workflow

Intro to HMC by Michael Betancourt

Bayesian Workflow by Gelman et. al.